Lorsqu’en Avril 1982, le professeur Dan Shechtman analyse le cliché de diffraction d’un échantillon métallique qu’il a obtenu avec son microscope électronique, il a du mal à croire à ses propres conclusions!

Lorsqu’en Avril 1982, le professeur Dan Shechtman analyse le cliché de diffraction d’un échantillon métallique qu’il a obtenu avec son microscope électronique, il a du mal à croire à ses propres conclusions! Car depuis plus de cent ans, les matériaux ordonnés étaient décrits par un empilement périodique et régulier d’atomes. Or son cliché indique sans ambiguïté qu’il observe un matériau ordonné mais non périodique, une étrange mosaïque d’atomes! Il vient de découvrir les quasicristaux, une découverte qui bouleverse un des concepts les mieux établis en cristallographie, et pour laquelle le prix Nobel de Chimie lui a été décerné en 2011.

Au moment de la découverte des quasicristaux la cristallographie et la diffraction sont des techniques bien établies pour étudier la structure des matériaux. On considère alors deux grandes classes de matériaux : les cristaux qui sont ordonnés et les matériaux amorphes comme les verres, dans lesquels les atomes ou les molécules sont disposées de manière aléatoire. Les cristaux sont constitués de l’empilement régulier et périodique d’une même cellule (un cube, un parallélépipède …) qui contient la ‘décoration’ atomique. C’est un peu comme un carrelage avec des pavés tous identiques. Toutes les formes de pavés (on parle de la symétrie des pavés) ne sont pas autorisées : on peut faire un pavage avec des carrés, des rectangles, des triangles, des hexagones, mais pas avec des pentagones (pavés à cinq cotés.) Pour les cristaux c’est la même chose et la symétrie 5 ou 10 était considérée comme ‘interdite’ : un cristal ordonné et périodique ne peut pas avoir la symétrie 5 ou 10.

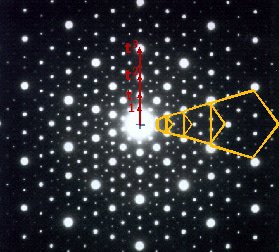
Or le cliché de diffraction observé par Dan Shechtman présente la signature d’un système ordonné mais avec une symétrie 10 interdite, comme le montre la figure!

Le quasicristal est donc un cristal ‘impossible’ ! Cette découverte, publiée deux ans après la première observation, dans un article co-signé par Dan Shechtman, Ian Blech, John Cahn et Denis Gratias a fait l’effet d’une bombe dans la communauté scientifique. Immédiatement après sa publication de nombreux articles expérimentaux et théoriques ont permis de comprendre ce paradoxe. La solution avait en fait été proposée par Roger Penrose en 1974, avec un pavage quasipériodique avec deux tuiles (voir figure) et dont Alan Mackay avait montré que son cliché de diffraction est identique a celui découvert plus tard par Dan Shechtman. Ce pavage de Penrose peut être généralisé à trois dimensions, comme l’ont en particulier proposé D. Levine et P. Steinhardt qui ont donné le nom ‘quasicristal’ à cette étrange mosaïque d’atomes.

Depuis cette découverte, de nombreux autres alliages quasicristallins ont été découverts, essentiellement en combinant différents métaux, mais également plus récemment des molécules organiques. Il s’agit donc bien d’un nouveau type d’ordre à grande distance, qui a nécessité de redéfinir la notion de cristal.

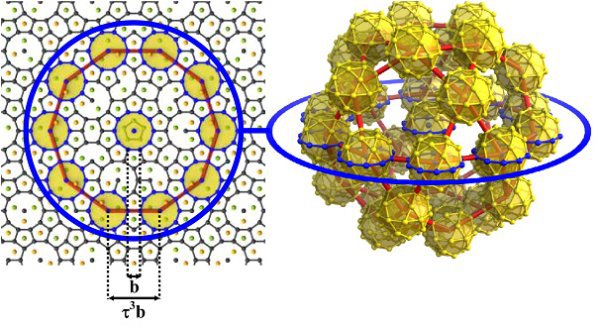
Cette découverte a suscité des recherches dans de très nombreux domaines : mathématiques, physique, chimie, sciences des matériaux. La structure atomique et les propriétés de ces matériaux sont maintenant mieux comprises, comme le montre la figure qui donne un aperçu de la structure d’un quasicristal dans le système CdYb. Les propriétés des quasicristaux permettent d’envisager un certain nombre d’applications, la plupart encore au stade du développement. Ainsi les alliages quasicristallins à base d’aluminium ont un coefficient de friction extrêmement faible pour des alliages métalliques : ils pourraient donc être utilisés comme revêtement. Ils peuvent aussi servir comme renfort mécanique dans des matériaux composites (aciers ou composites polymère/métal). Leurs propriétés électroniques sont également intéressantes pour des composés de substitution de métaux rares en catalyse chimique. Enfin la quasi- périodicité a déjà été utilisée pour construire des structures artificielles.